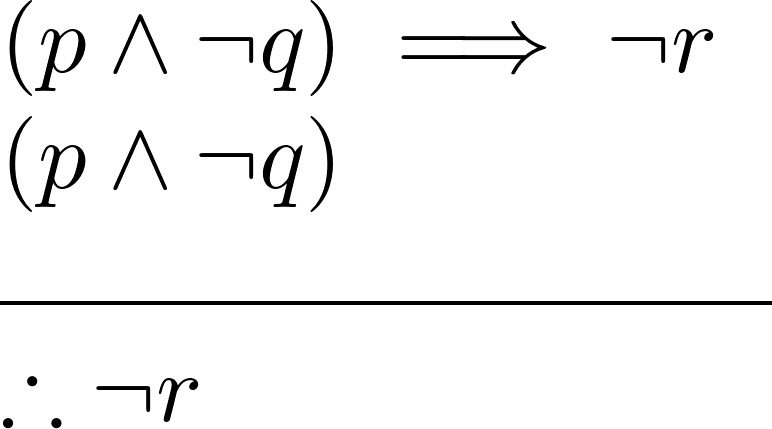Reglas de inferencia lógica

Modus ponendus ponens

Significa "modo que al afirmar, afirma", es una regla que nos permite eliminar la implicación de una prueba lógica o argumento. Formalmente se define como:

Comúnmente esta regla se escribe como:

Donde  es un símbolo que indica que q es una consecuencia sintáctica de  y p en algún sistema lógico. 

También puede escribirse como

Explicación:  el argumento tiene dos premisas o hipótesis (una condicional  y otra premisa p que indica que el antecedente a la alegación condicional es cierto).

Con ello, podemos concluir que el resultado de toda la fórmula o proposición es igual al mismo consecuente q.

Ejemplo con proposiciones literales:

Si hoy es lunes, entonces Ana tiene clase de matemáticas.

Hoy es lunes.

Por lo tanto, Ana tiene clase de matemáticas.

Ejemplo con proposiciones cualesquiera:

Modus tollendo tollens

Significa "modo que al negar, niega", es una regla que nos permite negar el consecuente de una prueba lógica o argumento. Formalmente se define como

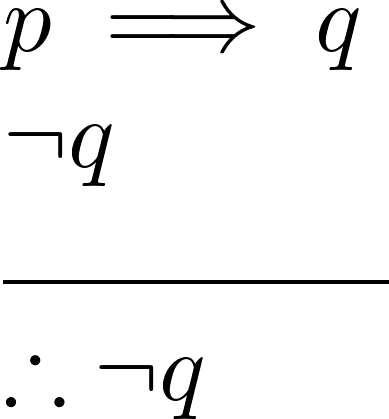
Explicación: esta regla establece que si una afirmación implica una segunda afirmación ()y la segunda afirmación no es verdadera (), entonces se puede deducir que la primera premisa no es verdadera.

Con ello, podemos concluir que el resultado de toda la fórmula o proposición es igual a la negación de la primera premisa consecuente .

Ejemplo con proposiciones literales:

Si ayer transfirieron el pago, entonces hoy tengo dinero en la cuenta.

Hoy no tengo dinero en la cuenta.

Por lo tanto, ayer no transfirieron el pago

Ejemplo con proposiciones literales: