Antiderivadas
Definición
El cálculo integral se ocupa del proceso inverso de derivación; es decir si tenemos la derivada de una función, el objetivo es hallar la función original.
Esta función original se denomina antiderivada o primitiva. Por ejemplo, considere la función ![]() :
:
![]()
Usted sabe por cálculo diferencial que:
![]()
Entonces ![]() es la antiderivada o función primitiva de la función
es la antiderivada o función primitiva de la función ![]() y está dada por:
y está dada por:
![]()
Y que cómo puede observar, se cumple que ![]()
Observación
Fíjese que existen varias (infinitas) antiderivadas de ![]() , a continuación se mencionan unas pocas:
, a continuación se mencionan unas pocas:
Por esta razón se habla de una antiderivada genérica de la función ![]() , y en este ejemplo se dice que la función
, y en este ejemplo se dice que la función ![]() dada por:
dada por:
![]()
Es la antiderivada de la función ![]() :
:
![]()
Donde es una constante. En este curso, ![]() representa a cualquier número real.
representa a cualquier número real.
Definición de integral indefinida
Considere la función ![]() continua en un intervalo; y la función
continua en un intervalo; y la función ![]() que es una primitiva de
que es una primitiva de ![]() .
.
Se dice que la expresión:
Es la integral indefinida de la función
El símbolo
En resumen, la expresión:
En nuestro curso, el objetivo de este tema es: hallar la primitiva genérica de una función.
Ejemplo
Pruebe que la función ![]() dada por: es una antiderivada de la función
dada por: es una antiderivada de la función ![]() dada por:
dada por: ![]() Luego de probar expréselo mediante una igualdad que contiene una integral.
Luego de probar expréselo mediante una igualdad que contiene una integral.
Para probarlo, derivamos ![]() , así:
, así:
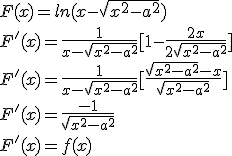
Y lo expresamos como una igualdad que contiene una integral.
![]()
Ejercicio de aplicación
| |
| Video 1: Definición de integral indefinida |
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0