Integración con condiciones iniciales
Definición
 En problemas prácticos, se requiere conocer una función primitiva única; y para esto es necesario conocer ciertos valores que toma la función para determinados valores de su dominio. Estos valores se suelen denominar condiciones iniciales o de frontera.
En problemas prácticos, se requiere conocer una función primitiva única; y para esto es necesario conocer ciertos valores que toma la función para determinados valores de su dominio. Estos valores se suelen denominar condiciones iniciales o de frontera.
Ejemplo
Si la función de ingreso marginal para el producto de un fabricante es:
![]()
Determine la función de demanda.
![]() es la función de ingreso y se tiene que
es la función de ingreso y se tiene que ![]() , donde
, donde ![]() es el precio por unidad y
es el precio por unidad y ![]() es el número de unidades. Entonces:
es el número de unidades. Entonces: ![]() es la función de demanda (
es la función de demanda ( ![]() solo en términos de
solo en términos de ![]() )
)
Para esto integramos la función de costo marginal:
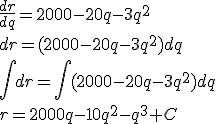
Donde ![]() es la constante de integración:
es la constante de integración:
El siguiente razonamiento nos conduce a obtener las condiciones iniciales:
“Cuando no se vende ninguna unidad, simplemente no hay ingreso”.
Por tanto: si: ![]() ,entonces:
,entonces: ![]() .
.
Si reemplazamos estos valores en nuestra primitiva genérica (función de ingreso ![]() ), podemos calcular
), podemos calcular ![]() .
.
![]()
Por tanto ![]() .
.
Entonces ya no tenemos infinitas primitivas, sino una sola primitiva: La función de ingreso del fabricante, así:
![]()
Y así determinamos la función de demanda del fabricante:
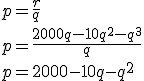
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0