Operaciones con conjuntos

UNION

Sean A y B conjuntos no vacíos, entonces la unión de A y B, se define:

A ∪ B = { x | x ∈A o x ∈B }

Su diagrama de Venn se representa mediante un rectángulo que en su interior posee 2 círculos que se  intersectan y representan a los conjuntos A y B que se encuentran sombreados.

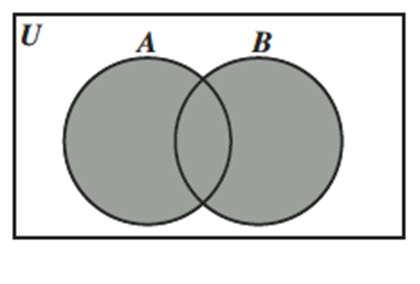
INTERSECCIÓN

Sean A y B conjuntos no vacíos, entonces la intersección de A y B se defi ne:

A ∩ B = { x | x ∈A y x ∈B }

Su diagrama de Venn se representa mediante un rectángulo que en su interior posee 2 círculos que se  intersectan y representan a los conjuntos A y B. En este caso se encuentra sombreado solamente la intersección o cruce de los 2 conjuntos.

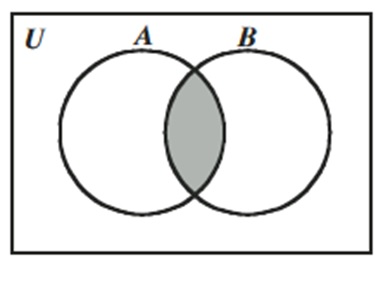
COMPLEMENTO

Sea U el conjunto universo y A un subconjunto de U, el complemento de A se define:

A´ = { x | x ∈ U y x ∉ A }

El conjunto solución contiene a los elementos que pertenecen a U y no pertenecen al conjunto A y se representa como A´ o Ac.

Su diagrama de Venn se representa mediante un rectángulo que en su interior posee 1 círculo que representa al conjuntos A . Se representa sombreando la región fuera del conjunto A y dentro del Rectángulo.

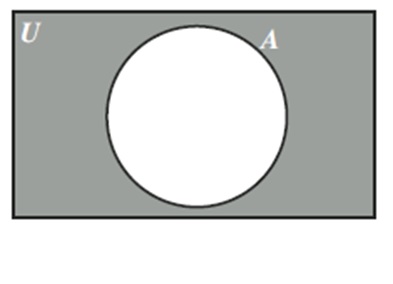
DIFERENCIA

Sean A y B conjuntos no vacíos, se define la diferencia como el conjunto que contiene a los elementos que pertenecen a A y que no pertenecen al conjunto B. La diferencia se representa como A − B.

A − B = A ∩ B c = { x | x ∈ A y x ∉ B }

Su diagrama de Venn se representa mediante un rectángulo que en su interior posee 2 círculos que se  intersectan y representan a los conjuntos A y B . Se encuentra sombreado unicamente la zona de A sin considerar la parte de intersección con B.

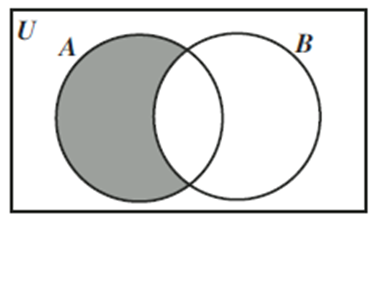
DIFERENCIA SIMETRICA

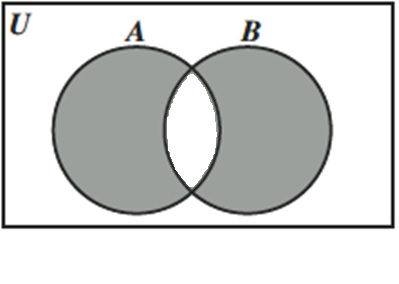
La diferencia simétrica entre los conjuntos A y B, que se denota como (A ♁ B), es el conjunto que contiene a todos los elementos que se encuentran en el conjunto A pero no están en el conjunto B y también a los elementos del conjunto B que no están en A. Dicho de otra manera, el conjunto (A♁B) contiene a todos los elementos que se encuentran en (A U B) pero que no están en (A ∩ B)

(A♁B)= x|( x ∈ A y x ∉ B) o ( x ∈ B y x ∉ A)

Su diagrama de Venn se representa mediante un rectángulo que en su interior posee 2 círculos que se  intersectan y representan a los conjuntos A y B . Se encuentra sombreado  A y B, pero no la intersección entre ellos.