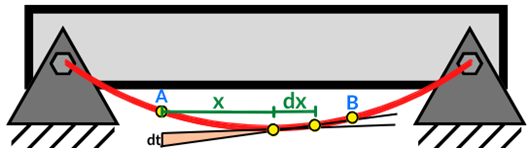
El primer teorema expresa que “la diferencia de pendientes entre dos puntos cualesquiera de una viga deformada es igual al área neta del diagrama de momentos flectores entre esos puntos, dividida por la constante de rigidez (EI) de la viga”. Esto se ejemplifica mediante la siguiente Figura, en donde se identifican los dos ángulos formados con respecto a los puntos A y B por las rectas tangentes que se han trazado, cuya diferencia es equivalente al área producida del área bajo la curva como se indicó en la sección 4.

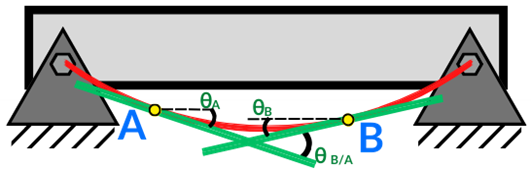
Se puede expresar mediante la Ecuación (6).

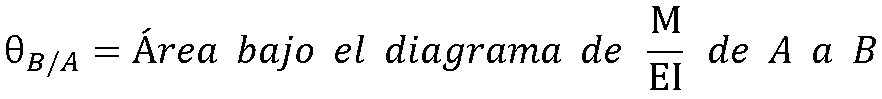(6)

El segundo teorema expresa que “el desplazamiento vertical de un punto de la curva elástica desde una tangente a la curva elástica en un segundo punto es igual al momento del área del diagrama de momentos que se encuentra entre los dos puntos, tomado alrededor del primer punto, dividido por la constante de rigidez (EI)”. Esto se ejemplifica mediante la Figura, en donde se identifican las dos rectas tangentes que se han trazado en los dos puntos centrales, cuya extensión hasta el punto A y medición vertical es equivalente a la deflexión alcanzada en términos diferenciales, 

Se expresa mediante la Ecuación (7).