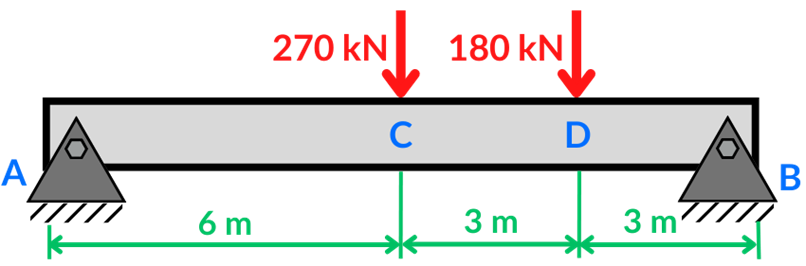
Determine la pendiente en los puntos A y B, y la deflexión en los puntos C y D de la viga mostrada en la Figura, empleando el método de momento de área. Considere que E=12.5 GPa y I=19200x10⁶ mm⁴.

Datos

E=12.5\ GPa=12.5x{10}^6\ \frac{kN}{m^2}

I=19200x{10}^6\ {\rm mm}^4=0.0192\ m^4L=12\ m

P_1=270\ kN

P_2=180\ kN

Resolución

Se determinan las reacciones en los apoyos mediante las condiciones de equilibrio de los cuerpos según la estática. Realizando una sumatoria de momentos en el punto B tenemos:

{\Sigma M}_B=0

{-R}_A\left(12\ m\right)+270\ kN\left(6\ m\right)+180\ kN\left(3\ m\right)=0

{-R}_A\left(12\ m\right)+1620\ kN\ m+540\ kN\ m=0

{-R}_A\left(12\ m\right)+2160\ kN\ m=0

{-R}_A\left(12\ m\right)=-2160\ kN\ m

R_A=\frac{-2160\ kN\ m}{-12\ m}=180\ kN

Aplicando sumatoria de Fuerzas en y se tiene:

{\Sigma F}_y=0

R_A-270\ kN-180\ kN+R_B=0

180\ kN-270\ kN-180\ kN+R_B=0

-270\ kN+R_B=0

R_B=270\ kN

Realizando un corte en el punto C y analizando el momento hacia la izquierda:

Realizando un corte en el punto D y analizando el momento hacia la derecha:

Con los valores de momentos encontrados se procede a realizar el diagrama de momentos, y se dividen en áreas como se muestra en la Figura.

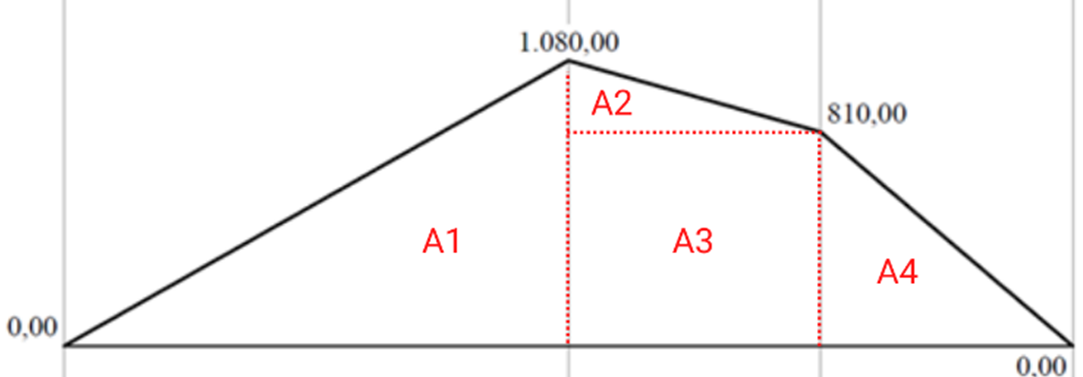
Pendiente A y B

Empleando la Ecuación 6 y 7, y reemplazando los valores de las áreas correspondientes del tramo AB según la Tabla de la sección 4.2 se tiene:

\theta_{B/A}=\frac{1}{EI}\left(A_1+A_2+A_3+A_4\right)=\frac{1}{EI}\left[\frac{6\left(1080\right)}{2}+\frac{3\left(1080-810\right)}{2}+3\left(810\right)+\frac{3\left(810\right)}{2}\right]

\theta_{B/A}=\frac{7290}{EI}

y_{B/A}=\frac{1}{EI}\left(A_1{\overline{x}}_1+A_2{\overline{x}}_2+A_3{\overline{x}}_3+A_4{\overline{x}}_4\right)

y_{B/A}=\frac{1}{EI}\left[\frac{6\left(1080\right)}{2}\left(6+\frac{6}{3}\right)+\frac{3\left(1080-810\right)}{2}\left(3+\frac{2\left(3\right)}{3}\right)+3\left(810\right)\left(3+\frac{3}{2}\right)+\frac{3\left(810\right)}{2}\left(\frac{6}{3}\right)\right]

y_{B/A}=\frac{41310}{EI}

Considerando que la pendiente en A se forma hasta la desviación vertical en B como se muestra en la Figura se representa mediante la expresión:

tan{\theta_A}=\frac{y_{B/A}}{L}

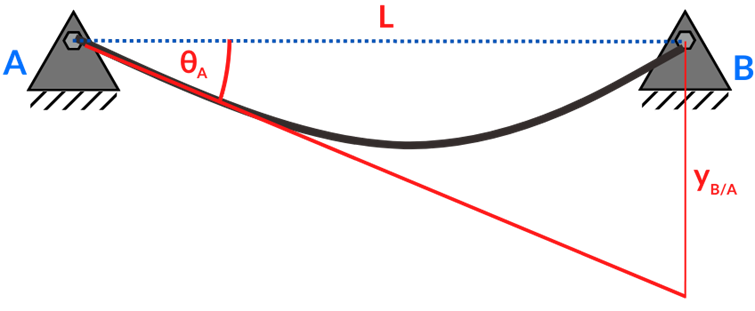
Si la pendiente es pequeña tan θ_A ≈ θ_A , entonces

\theta_A=\frac{y_{B/A}}{L}=\frac{\frac{41310}{EI}}{12}=\frac{3442.50}{EI}=\frac{3442.50}{12.5x{10}^6\left(0.0192\right)}=0.01434\ rad

Como θ_A está ubicado en sentido horario se considera negativo.

\theta_A=-0.01434\ rad

Considerando θ_B/A=θ_B-θ_A que  se puede despejar θ_B.

\theta_B=\theta_{B/A}+\theta_A=\frac{7290}{EI}+\left(-0.01434\right)=\frac{7290}{12.5x{10}^6\left(0.0192\right)}-0.01434=0.016035\ rad

Deflexión en C

Empleando la Ecuación 7, y reemplazando los valores de las áreas correspondientes del tramo AC según según la Tabla de la sección 4.2 se tiene:

y_{C/A}=\frac{1}{EI}\left(A_1{\overline{x}}_1\right)=\frac{1}{EI}\left[\frac{6\left(1080\right)}{2}\left(\frac{6}{3}\right)\right]=\frac{6480}{EI}

Considerando que la pendiente en A se forma hasta la desviación vertical en C como se muestra en la Figura se representa mediante la expresión:

tan{\theta_A}=\frac{y_C+y_{C/A}}{6}

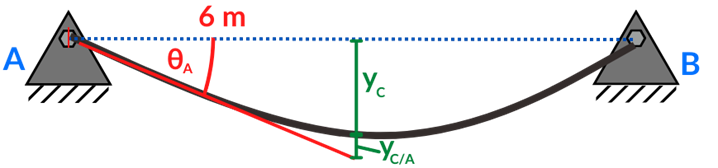
Si la pendiente es pequeña tan θ_A ≈ θ_A, entonces

\theta_A=\frac{y_C+y_{C/A}}{6}

6\theta_A=y_C+y_{C/A}

y_C=6\theta_A-y_{C/A}

y_C=6\left(0.01434\right)-\frac{6480}{12.5x{10}^6\left(0.0192\right)}=0.05904\ m=59.04\ mm

Como la deflexión y_C va hacia abajo  se considera negativo.

y_C=-59.04\ mm

Deflexión en D

Empleando la Ecuación 7, y reemplazando los valores de las áreas correspondientes del tramo BD según la Tabla de la sección 4.2 se tiene:

y_{D/B}=\frac{1}{EI}\left(A_4{\overline{x}}_4\right)=\frac{1}{EI}\left[\frac{3\left(810\right)}{2}\left(\frac{3}{3}\right)\right]=\frac{1215}{EI}

Considerando que la pendiente en B se forma hasta la desviación vertical en D como se muestra en la Figura se representa mediante la expresión:

tan{\theta_B}=\frac{y_D+y_{D/B}}{3}

Si la pendiente es pequeña tan θ_B ≈ θ_B, entonces

\theta_B=\frac{y_D+y_{D/B}}{3}

3\theta_B=y_D+y_{D/B}

y_D=3\theta_B-y_{D/B}

y_D=3\left(0.016035\right)-\frac{1215}{12.5x{10}^6\left(0.0192\right)}=0.04304\ m=43.04\ mm

Como la deflexión y_D va hacia abajo  se considera negativo.

y_D=-43.04\ mm

Determine la deflexión máxima mediante el método de momento de área en la viga mostrada en la Figura, empleando el método de momento de área. Considere que EI=50 kN mm².

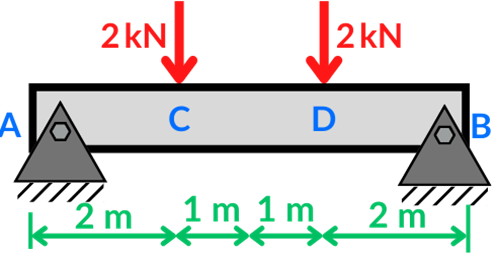
Datos

EI=50\ kN\ m^2

L=6\ mP=2\ kN

Resolución

Se determinan las reacciones en los apoyos mediante las condiciones de equilibrio de los cuerpos según la estática. Realizando una sumatoria de momentos en el punto B tenemos:

{\Sigma M}_B=0

{-R}_A\left(6\ m\right)+2\ kN\left(4\ m\right)+2\ kN\left(2\ m\right)=0

{-R}_A\left(6\ m\right)+8\ kN\ m+4\ kN\ m=0

{-R}_A\left(6\ m\right)+12\ kN\ m=0

{-R}_A\left(6\ m\right)=-12\ kN\ m

R_A=\frac{-12\ kN\ m}{-6\ m}=2\ kN

Por simetría de la viga se deduce:

R_B=R_A=2\ kN

Realizando un corte en el punto C y analizando el momento hacia la izquierda:

Si se realiza un corte en el punto C hacia la derecha por simetría de la viga se deduce:

M_D=4\ kN\ m

Con los valores de momentos encontrados se procede a realizar el diagrama de momentos, y se dividen en áreas como se muestra en la Figura.

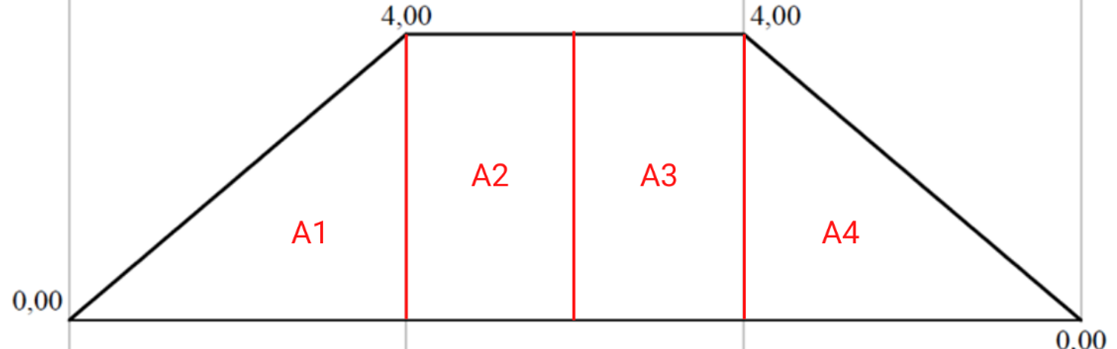
Empleando la Ecuación 6 y 7, y reemplazando los valores de las áreas correspondientes del tramo AB según la Tabla de la sección 4.2 se tiene:

y_{\frac{L}{2}/A}=\frac{1}{EI}\left(A_1{\overline{x}}_1+A_2{\overline{x}}_2\right)=\frac{1}{EI}\left(\frac{2\left(4\right)}{2}\left(\frac{2\left(2\right)}{3}\right)+1\left(4\right)\left(2+\frac{1}{2}\right)\right)=\frac{46}{3EI}

Considerando que la pendiente en la mitad de la viga es cero la desviación vertical es igual a la deflexión obtenida en ese punto como se muestra en la Figura se representa mediante la expresión:

y_{\frac{L}{2}/A}=y_\frac{L}{2}=\frac{22}{3EI}=\frac{22}{3\left(50\right)}=0.3067\ m=306.7\ mm

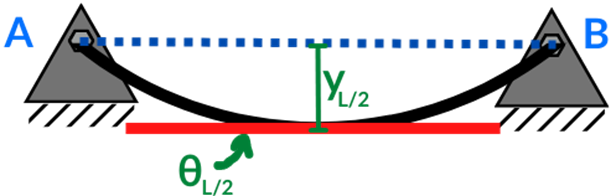
Como la deflexión en la mitad de la viga va hacia abajo se considera negativa.

y_\frac{L}{2}=-306.7\ mm

Determine la deflexión en el punto C mediante el método de momento de área. Considere que EI=215 kN m².

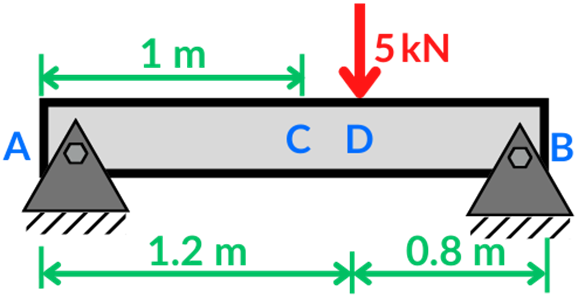
Datos

EI=215\ kN\ m^2

L=2\ mP=5\ kN

Resolución

Se determinan las reacciones en los apoyos mediante las condiciones de equilibrio de los cuerpos según la estática. Realizando una sumatoria de momentos en el punto B tenemos:

{\Sigma M}_B=0

{-R}_A\left(2\ m\right)+5\ kN\left(0.8\ m\right)=0

{-R}_A\left(2\ m\right)+4\ kN\ m=0

{-R}_A\left(2\ m\right)=-4\ kN\ m

R_A=\frac{-4\ kN\ m}{-2\ m}=2\ kN

Aplicando sumatoria de Fuerzas en y se tiene:

{\Sigma F}_y=0

R_A-5\ kN+R_B=0

2\ kN-5\ kN+R_B=0

-3\ kN+R_B=0

R_B=3\ kN

Realizando un corte en el punto D y analizando el momento hacia la derecha:

Con los valores de momentos encontrados se procede a realizar el diagrama de momentos, y se dividen en áreas como se muestra en la Figura.

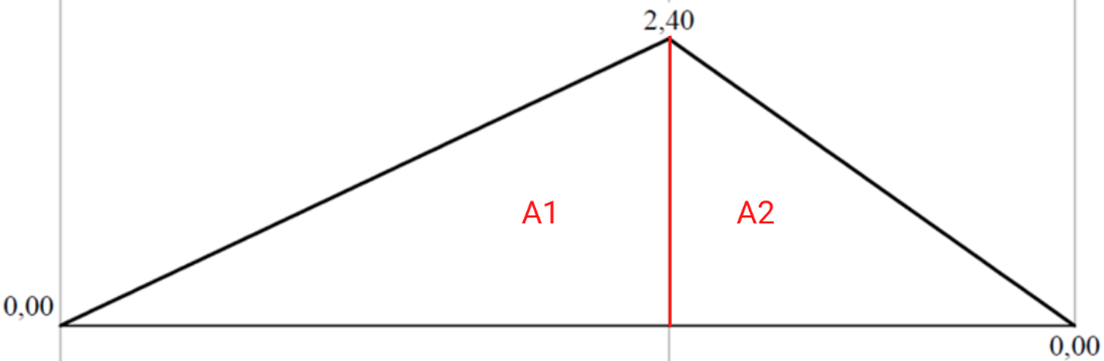
El momento en el punto C se puede determinar mediante la proporcionalidad de la pendiente de manera que:

tan{\theta}=\frac{2.4}{1.2}=\frac{M_C}{1}

M_C=2\ kN\ m

Empleando la Ecuación 7, y reemplazando los valores de las áreas correspondientes del tramo AB según la Tabla de la sección 4.2 se tiene:

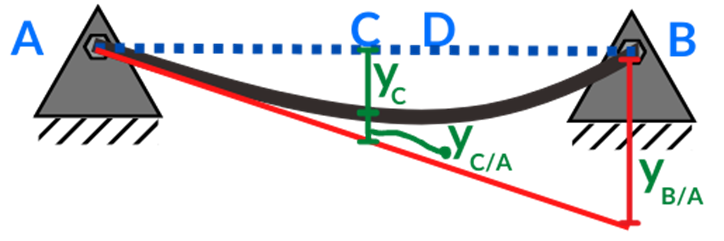
y_{B/A}=\frac{1}{EI}\left(A_1{\overline{x}}_1+A_2{\overline{x}}_2\right)=\frac{1}{EI}\left[\frac{1.2\left(2.4\right)}{2}\left(0.8+\frac{1.2}{3}\right)+\frac{0.8\left(2.4\right)}{2}\left(\frac{2\left(0.8\right)}{3}\right)\right]=\frac{2.24}{EI}Considerando que la pendiente en A se forma hasta la desviación vertical en B y a 1 m como se muestra en la Figura se representa la proporcionalidad geométrica mediante la expresión:

tan{\theta_A}=\frac{y_{B/A}}{L}=\frac{y}{1}

\frac{\frac{2.24}{EI}}{2}=\frac{y}{1}

y=\frac{\frac{2.24}{EI}}{2}=\frac{1.12}{EI}

Empleando la Ecuación 7, y reemplazando los valores de las áreas correspondientes del tramo AC según la Tabla de la sección 4.2 se tiene:

y_{C/A}=\frac{1}{EI}\left(A\right)=\frac{1}{EI}\left[\frac{1\left(2\right)}{2}\left(\frac{1}{3}\right)\right]=\frac{1}{3EI}

Considerando que y_C/A=y-y_C se puede despejar .

y_C=y-y_{C/A}=\frac{1.12}{EI}-\frac{1}{3EI}=\frac{0.7867}{EI}=\frac{0.7867}{215}=0.003659\ m=3.66\ mm